Maurits Escher, l’illusion de l’impossible

Maurits Escher est un "mathémagicien" qui a réalisé des œuvres aux constructions réalistes et pourtant physiquement irréalisables, mêlant art et mathématiques. Son style unique et original s'appuie sur la manipulation des formes, des espaces et des perspectives, en explorant des thèmes tels que les constructions impossibles, les explorations de l’infini, les pavages et les métamorphoses.

Des paysages à l'architecture, un voyage graphique

Le néerlandais Maurits Cornelis Escher est un dessinateur, illustrateur de livres, créateur de tapisseries, mais principalement connu en tant qu'artiste graveur. Né le 17 juin 1898, il meurt en 1972 aux Pays-Bas, laissant derrière lui plus de 400 estampes et 2000 dessins. Jusqu'à ses 13 ans, il apprend le métier de charpentier, ce qui lui donne des notions de construction 3D dans l'espace. D'abord inspiré par l'architecture, il rentre dans une école spécialisée dans ce domaine et dans l'art, à Haarlem. Il rate ses examens à cause de problèmes de santé, avant de se tourner finalement vers les arts décoratifs, sous la direction de Samuel Jessurun de Mesquita, un artiste qui l'initie à la gravure sur bois et dont il restera proche jusqu'à ce que cet ami et sa famille se fasse décimer par les nazis en 1944.

Ci-dessous, des gravures de Mesquita, suivies d’œuvres d'Escher. On retrouve chez les deux artistes le travail de tracé, de simplicité dans la forme contrastée en aplat, et de géométrie.

Gravures de Samuel Jessurun de Mesquita : Marabout, 1909 — Femme, 1929 — Hibou duc, 1915 — Extase, 1922 — Héron, 1928

Gravures de M.C. Escher, 1921 : La superstition de la prostituée — Femme assise nue — Le parfum

Escher puise également son inspiration chez Giovanni Battista Piranesi, un graveur italien du XVIIIe siècle, célèbre pour ses vues fantastiques et vertigineuses de Rome et ses prisons imaginaires.

C'est d'abord la campagne Italienne, ses villes denses, ses côtes dramatiques et ses routes sinueuses qui inspirent M.C. Escher pour ses dessins. Avec ces paysages, il explore la technique du "dessin gratté" en recouvrant sa feuille d'encre de lithographie (une encre grasse) qu'il vient gratter avec une pointe. De son studio à Rome, où il vit et grave, il s'inspire des détails des bâtiments, en proposant parfois des perspectives étonnantes et simultanées dans deux directions opposées.

En 1922 puis en 1936 Maurits Escher visitera l'Espagne, dont l'architecture le marquera profondément et aura une grande influence sur son travail. Escher s'inspire aussi des peintres primitifs flamands, des jeux d'optique (on parlera de ces deux inspirations plus bas), du bestiaire médiéval et fantastique (il dessinera de nombreux dragons ou bêtes mythologiques), ou encore du surréalisme, dont il est contemporain. Il existe dans son œuvre globale une certaine fascination pour l'infini, que ce soient dans les pavages ou dans ses dessins mathématiques.

La beauté des monuments de l’art islamique, notamment les motifs répétitifs et géométriques des carreaux de l’Alhambra à Grenade, un palais maure du XIVe siècle, sont une révélation. Les creux et les imbrications des bas-reliefs, des créneaux et des carreaux lui inspirent des formes abstraites et fantaisistes jouant avec le négatif/positif, à tel point que le pavage devient une véritable obsession. En Andalousie, il étudie aussi la mosquée de Mezquita à Cordoue, d'après lesquels il fait plusieurs croquis d'observation.

Avec sa femme et ses enfants, Escher vivra en Italie (qu'ils quitteront avec la montée du fascisme), en Suisse, puis en Belgique avant de revenir s'installer aux Pays-Bas en 1941.

Un maître de la gravure

Escher utilise différentes techniques comme la gravure sur bois au début de sa carrière, la manière noire —ou mezzotinte— à partir de 1930 (gravure en taille-douce avec un grainage très subtil qui permet d'éviter de faire des demi-teintes en hachures ou petits points, et crée des tons riches et profonds), la lithographie (qui repose sur le principe chimique de la répulsion du gras et de l'eau, où l'on dessine sur une pierre calcaire absorbante avec un crayon gras ou un pinceau, avant d'humidifier la pierre et de l'encrer, laissant les parties dessinées retenir l'encre pour l'impression), mais aussi la gravure sur linoléum (dans laquelle on creuse le support mou avec des outils, avant d'encrer ce qui reste à la surface, pour impression). Escher a également illustré des livres, des tapisseries, des timbres et des œuvres murales.

Un autre monde, MC Escher. A gauche, lithographie de 1947, reprenant l'architecture impossible de celle de droite en mezzotinte, 1946

Une obsession pour les pavages géométriques

Dans les années 20, à la suite de son voyage à l'Alhambra, alors qu'il est encore étudiant, il développe une théorie : la "division régulière du plan". Il démontre ainsi qu'en utilisant des motifs répétitifs et géométriques on peut découper l'espace sans laisser de vide entre chaque formes, en pavages périodiques. C'est cette même technique qui est utilisée dans les pavages de carreaux pour répéter des motifs décoratifs, et en cristallographie pour représenter les formes physiques des atomes de cristaux. C'est son frère, Berend George, pionnier de la géologie expérimentale, qui l'a initié à la cristallographie. Escher crée en 1922 son premier motif composé de huit têtes (ci-dessous) qu'il vient imprimer séparément en carrés imbriqués :

M.C. Escher, huit têtes, 1922, gravure sur bois

En cristallographie, la structure d'un cristal s'articule autour d'une unité répétée (dans le cas d'Escher, d'un motif) dans toutes les directions, avec des propriétés de symétrie par centres, axes de rotation inverses ou directs, ou des miroirs. Cela permet la répétition du motif à l'infini et sans vide, représenté en 3D par des grilles de cubes (comme ci-dessous), ou en 2D par des pavages périodiques.

Cristallographie d'un atome de sel marin fossilisé — Division cubique de l'espace, 1952

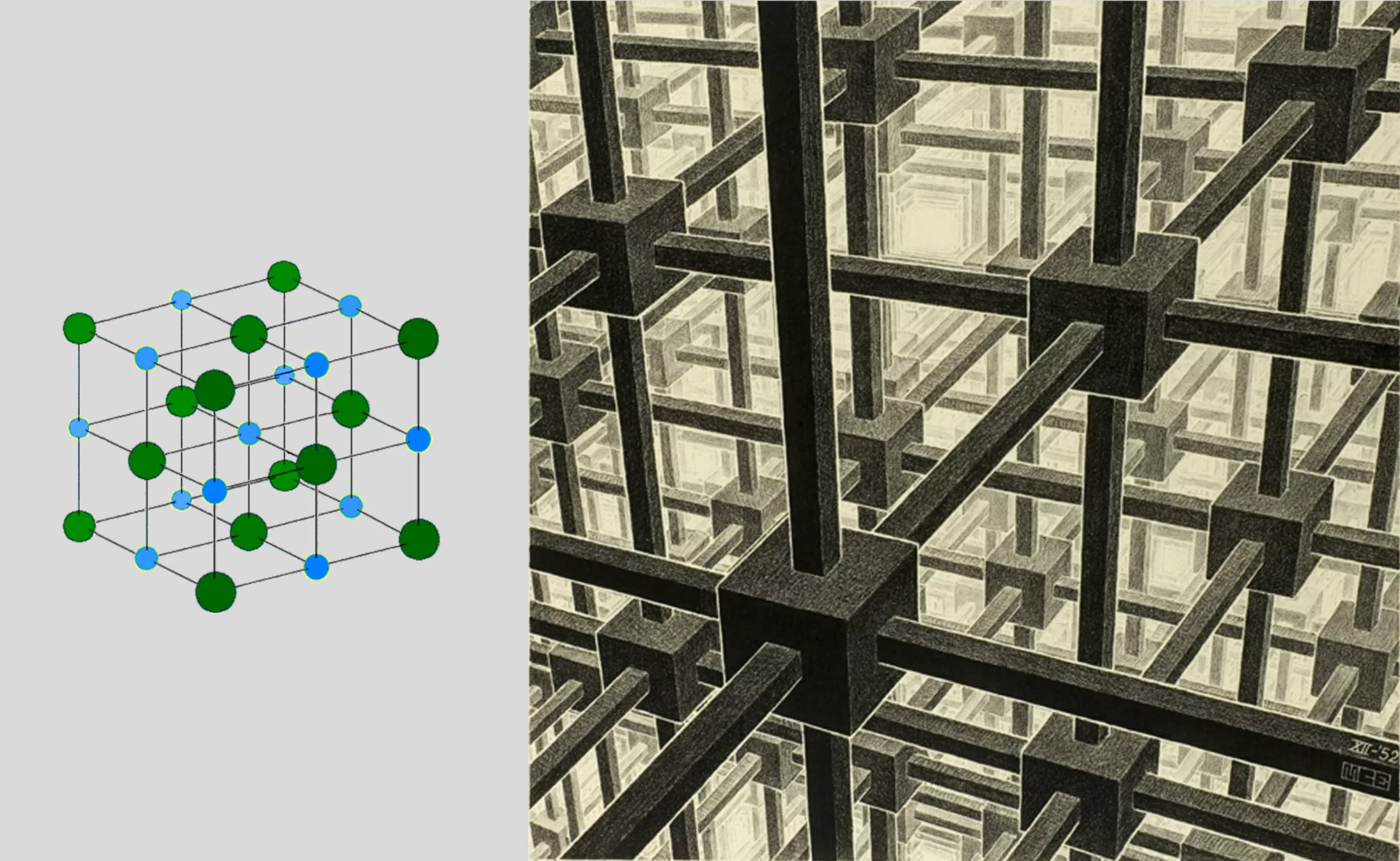
Escher explique sa théorie de division régulière du plan comme ceci : "un plan, qui devrait être considéré comme illimité de tous les côtés, peut être rempli ou divisé en figures géométriques similaires qui se côtoient de tous les côtés sans laisser d'espaces vides. Ceci peut être poursuivi à l'infini selon un nombre limité de systèmes". Il joue avec diverses formes qu'il imbrique ou fait évoluer.

M.C. Escher, Poissons volants, 1954 — Oiseau poisson, 1938

À cette même époque, après son premier voyage en Andalousie, Escher commence une série de gravures appelées "métamorphoses" dans lesquelles il fait muer une forme, un animal ou en personnage en un autre, un oiseau en un âne par exemple. Dans le visuel ci-dessous, on voit une première série allant de la ville fortifiée à la poupée chinoise (1937), suivie d'une autre métamorphose de 1939-1940 coupée ici en 4 pans pour en voir les détails, du damier aux lézards, à la ruche, aux abeilles, poissons, oiseaux, damier et toits de ville avant de terminer en échiquier.

Cette quête de la mutation de la forme associée ses pavages sans vide le pousse à développer des systèmes mathématiques de motifs qui évoluent infiniment.

M.C. Escher, Chevaux et oiseaux, 1949 — Verbum, 1942

M.C. Escher, Miroir magique, 1946

M.C. Escher, Chevaliers, 1957 - 1946

C'est en quittant l'Italie en 1935 qu'il abandonne l'étude des paysages pour créer ce qu'il appelle de "l'imagerie mentale", l’art de créer des représentations visuelles qui défient les lois de la physique, de la logique et de la perspective...

Trompe-l’œil et magie mathématique

Magicien fasciné par les mathématiques, qu’il considérait comme la source de la beauté et de l’harmonie, Escher étudie les notions de géométrie, de topologie, de logique, de fractales, de nombres complexes et de dimensions. Il utilise les mathématiques pour créer des effets visuels surprenants, tels que des paradoxes, des illusions et des formes infinies. Georges Perec écrit à propos du trompe-l’œil dans l’œil ébloui : "On nous a fait pendant un moment douter de nos sens, et dans cette brève et éphémère mystification se révèle quelque chose qui est de l’ordre du magique, du merveilleux, un étonnement délicieusement borgésien…"

On trouve plusieurs "objets impossibles" ou "paradoxes" dans ses sources d'inspiration, comme le triangle et l'escalier de Penrose, le ruban de Möbius, et le cube de Necker, quatre formes 2D qui donnent l'illusion de 3D grâce à des jeux d'optique, mais qui ne peuvent exister en volume dans le monde réel. Son inspiration l'amène à collaborer mutuellement avec des mathématiciens ou scientifiques qui utilisent aussi ses oeuvres pour illustrer leurs notions, et lui proposent des idées et des modèles.

Comme l'écrit Gilles Methel dans "Un art magique ?", Entrelacs : "ce n’est pas la représentation de l’espace qui est question mais la façon de l’habiter en défiant les lois de la gravitation." Maurits Escher utilise les mathématiques pour philosopher sur l'absurdité du temps qui passe et sur l'espace, souvent représentés en boucle infinie qui frôle souvent l'absurde. Des chutes d'eau qui remontent, des escaliers qui se succèdent dans des rondes sans fin, des animaux qui changent de forme et se réincarnent... son imaginaire transcende les limites du cerveau dans des illusions qui font perdre la tête.

M.C. Escher, Belvédère, 1958 — Montée, descente, 1960

Escher s'inspire aussi de la géométrie hyperbolique de Poincaré en répétant indéfiniment des motifs dans des sphères, à la manière des projections stéréographiques utilisées elles-aussi en cristallographie. Le terme fractales, qui explique ce principe de répétition d'un motif à échelles variables, sera pourtant inventé 2 ans après la mort d'Escher.

Les sphères et les reflets

Escher développe une capacité impressionnante pour dessiner les sphères et notamment les reflets, dans lesquelles il déforme la perspective en courbes. Ses méthodes sont si précises et parfaites qu'on dirait qu'il utilise un logiciel, mais tout est fait à la main. On vous explique juste après comment faire vos sphères sous illustration. Il puise cette inspiration auprès des grands maîtres flamands du XVe (étant lui-même flamand), comme Jan Van Eyck, Quentin Metsys ou Petrus Christus, qui ont peint de nombreux tableaux aux miroirs de sorcière, mais aussi d'un autoportrait du peintre italien "Parmigianino" du XVIe siècle. La difficulté d'un tel rendu prouve sa grande maîtrise des courbes, d'autant plus qu'il grave ses motifs, ce qui rend le travail plus minutieux encore que le dessin.

Quinten Metsys, Le préteur et sa femme (détail), 1514 — Jan van-Eyck, Portrait dit des époux Arnolfini (détail), 1434 — Parmigianino, Autoportrait au miroir, 1524 — Christu, Un orfèvre dans son atelier, peut-être Saint Éloi (détail), 1449

M.C. Escher, Main à la sphère réfléchissante, 1935 — Autoportraits

M.C. Escher, Trois sphères, 1946

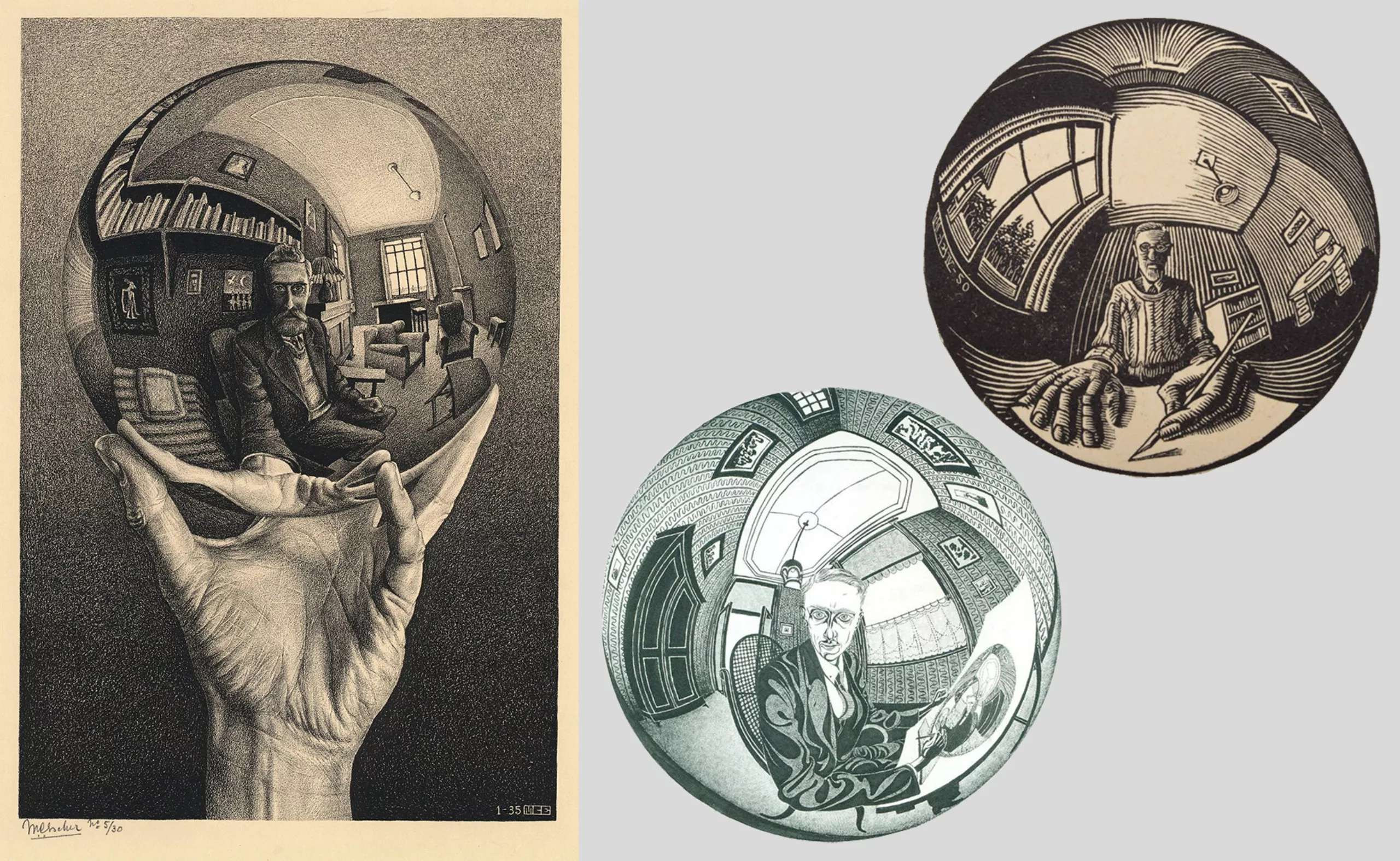
Aujourd'hui, on peut faire en quelques minutes (heures) un rendu quasi similaire de l’œuvre Trois sphères (1945) sur Illustrator... Il faut créer un arc de cercle, puis sélectionner l'option 3D "révolution", et cocher "bord droit". Il faut ensuite créer un motif de traits blancs en triangle (de large à fin) sur un fond de rectangle noir, et l'appliquer en "placage" à la sphère. Assez simple en théorie mais la création du motif peut prendre un peu de temps. La notre n'est d'ailleurs pas parfaite. Les options 3D permettent aussi d'ajouter n'importe quelle texture à une sphère.

La perspective courbe et infinie

Nicolas de Cues, dans Le tableau ou la vision de Dieu en 1453, écrivait que "L'angle décrit par ton œil, mon Dieu, n'est pas limité dans l'espace mais est infini; il est le cercle, plus encore: la sphère infinie. Car ton regard est l’œil de la sphéricité et de la perfection infinie." Sans pour autant se prendre pour Dieu, Escher n'était pas sans savoir que les mathématiques et le divin ont été souvent liées, surtout au XVe lorsque l'on considérait que le Créateur Chrétien était "le grand horloger du monde" et que les Mathématiques en étaient le langage d'expression. L’œuvre commune de Pacioli et Da Vinci, De Divina Proportione, dans laquelle Da Vinci illustre les proportions "divines" des figures mathématiques ou même des caractères typographiques Romains, est d'ailleurs une grande source d'inspiration pour Escher (illustrations ci-dessous, avec en 1e ligne les illustrations de Da Vinci, et dessous celles de Escher) qui en reprend les formes géométriques dans ses oeuvres, bien humaines.

Avec les sphères, il s'attaque à la perspective en lignes droites qui est incorrecte d'après lui, car elle ne prend pas en compte la perspective rétinienne qui, elle, est courbe. Il appelle cette trouvaille "perspective cylindrique", et en fait la démonstration dans une œuvre inachevée, "Exposition d'estampes" en 1956, dont le point central est laissé blanc (avec sa signature au centre). L’œuvre a pu être complétée en 2004 grâce à l'équipe de mathématiciens de l'université de Leyde et l'artiste néerlandaise Jacqueline Hoftra, en observant une combinaison de fonctions mathématiques suivant les angles de la grille d'Escher ce qui a permis de créer un tourbillon infini dans le tableau. Cet effet de mise en abyme, appelé effet Droste, vient de la publicité du cacao Droste dans laquelle on voit une nonne qui tient un plateau avec une boîte de poudre de cacao, sur laquelle apparaît la même image, et qui donc nous plonge à l'infini dans le visuel. Face à la perplexité qu'il engendrait souvent chez ses admirateurs, Escher aimait répondre : « tout cela n'est rien comparé à ce que je vois dans ma tête ! ».

Escher graphiste

On le sait moins, mais M.C. Escher a aussi réalisé plusieurs logos ou illustrations pour des livres, en tant que graphiste. On lui doit aussi quelques papiers cadeaux en jeux de lettres (en haut à droite pour la marque Zingone et à sa gauche pour de Bijenkorf, en 1933), et la réalisation de cartes de vœux pour des amis à lui.

On voit ci-dessous en rouge un logo extrêmement détaillé pour un restaurant chinois et indien (1944), une de ses premières linogravures pour un ex-libris représentant un chevalier en vert en noir (1918), une autre aux deux cigognes (1917), un troisième ex-libris de 1946 en gravure sur bois, en haut à gauche, et trois affiches en bas à droite pour des invitations d'exposition et un club d'échecs (1931 et 1936). Cliquez sur l'image pour la voir en grand.

Cartes de vœux pour Eugène et Willy Strens, élément terre en 1953, élément air en 1954, Escher, gravures sur bois.

Cartes de vœux pour Eugène et Willy Strens, élément feu en 1956 et eau en 1956, Escher, gravures sur bois.

Escher a été longtemps négligé par le monde de l’art, qui le considérait comme un simple illustrateur extra-plastique, ou un artiste populaire. Ce n’est qu’à la fin de sa vie qu’il a commencé à recevoir une reconnaissance internationale et une appréciation critique. À 70 ans, ses œuvres commencent à être exposées dans de nombreux musées et galeries, et sont reproduites dans de nombreux livres et articles. Aujourd'hui, il est renommé et reconnu dans de nombreux pays.

L'influence d'Escher dans le cinéma, les jeux, et les logos

Les œuvres d'Escher ont également influencé la culture populaire, notamment le cinéma, la musique, la littérature, les jeux vidéo... Les lithographies le plus souvent détournées sont Relativity (1953), avec ses escaliers impossibles, et Convexe et concave (1955) dans laquelle les escaliers mènent à la fois en haut et en bas, dans une illusion parfaite :

On retrouve par exemple ce principe d'étages impossibles dans l'étrange film Labyrinth de Jim Henson (1986) avec David Bowie qui se joue de la perspective :

...mais aussi dans Une nuit au musée : le secret des Pharaons (2014) de Shawn Levy dans lequel le personnage principal plonge dans Relativity. La scène des escaliers tournants d'Harry Potter à l'école des Sorciers y fait aussi référence.

Christopher Nolan, dont on parlait dans notre article sur les ambigrammes, est lui aussi un grand fan des gravures d'Escher. Il détourne à sa façon les oeuvres Gravity, Relativity, Division cubique de l'espace ou House of stairs dans Inception (2010) avec la ville qui se replie sur elle-même, et dans Interstellar (2014) dans la Station Cooper, ou dans la scène du tesseract qui rappelle les structures cristallographiques en 3D.

Le Tesseract, Interstellar, une scène qui rappelle la structure 3D de Division cubique de l'espace de Escher

Nolan a dit être inspiré par "la manière dont les choses se connectent ou le brouillage des frontières entre l'art et la science, et l'art et les mathématiques" dans les oeuvres d'Escher.

On retrouve aussi l'influence d'Escher dans le Seigneur des anneaux, avec les mines de la Moria ou le départ des elfes (coucou les fans) qui rappellent la Procession de la crypte de 1927, ou encore le feu d'artifice de la soirée de Bilbo, inspirée de la gravure de 1933.

Plus récemment, on a retrouvé l'influence de Relativity dans la série Squid game qui a repris dans ses décors les perspectives des escaliers impossibles. Côté jeux, Monument Valley dont on parlait il y a quelque temps dans notre article sur les jeux mobiles graphiques se base sur des perspectives impossibles avec des escaliers tournants qui ouvrent de nouveaux chemins.

Un amateur a même créé un lego reprenant l’œuvre d'Escher. Et il y aurait encore sûrement des centaines de références, n'hésitez pas à les partager en commentaire.

Côté logos, on aime imaginer le lien entre la pelure d'Orangina et Pelure d'Escher, mais la première paraît en 1953, alors que l’œuvre a été créee 2 ans plus tard. À l'époque de la création du logo en peau d'orange, le gouvernement français ne permettait pas la représentation de fruits sur des produits contenant moins de 25% de jus, et le graphiste de l'affiche, Villemot, a contourné la chose en dessinant la peau du fruit.

Ici encore, le logo Woolmark de Grignani (1964) semble être une déclinaison du Noeud d'Escher (1965), mais les deux n'ont à priori aucun lien, à part l'amour des lignes et des formes géométriques !

Escher est considéré comme l’un des plus grands artistes graphiques du XXe siècle, en tant que maître de l’illusion et de la géométrie, bien avant l'avènement des images générées par ordinateur. Sa patience infinie a créé des œuvres fascinantes et énigmatiques, qui défient la logique et l’imagination, et qui invitent à la réflexion et à l’émerveillement. « Je ne peux pas m’empêcher de me demander et d’admirer les lois de la nature, qui se manifestent dans les plus petites choses, » disait-il.

Pour aller plus loin :
Escher in heit paleis
http://sweetrandomscience.blogspot.com/2012/11/escher-et-les-sciences-lobsession-de.html
https://www.illustrationhistory.org/essays/the-hidden-emotions-in-m.c-eschers-artwork
https://journals.openedition.org/entrelacs/2015